1.8 Determining Limits Using the Squeeze Theorem

1.8 Determining Limits Using the Squeeze Theorem

Welcome back to AP Calculus with Fiveable! This topic focuses on determining the limit of a function based on information given about other functions that bound it. We’ve worked through determining limits through algebraic manipulation, graphs, and tables, so let's keep building our limit skills. 🙌

⌛ Squeeze Theorem

Before we get into the nitty gritty, be sure to review some of the content we’ve already went over!

📚 Background Knowledge

To effectively use the Squeeze Theorem, you should be familiar with:

• Limits: Understanding how functions behave near a specific value.
• Basic Function Behavior: Knowledge about how functions like sine, cosine, exponential, etc., behave for different inputs.

🧩 What is the Squeeze Theorem?

The squeeze theorem states that if $\textcolor{red}{f(x)} \leq \textcolor{blue}{ g(x)} \leq \textcolor{green}{h(x)}$ and $\lim_{{x \to a}} f(x) = \lim_{{x \to a}} h(x) = \textcolor{orange}{L}$, then $\lim_{{x \to a}} g(x)$ must also $= \textcolor{orange}{L}$. Take a look at the visual below!

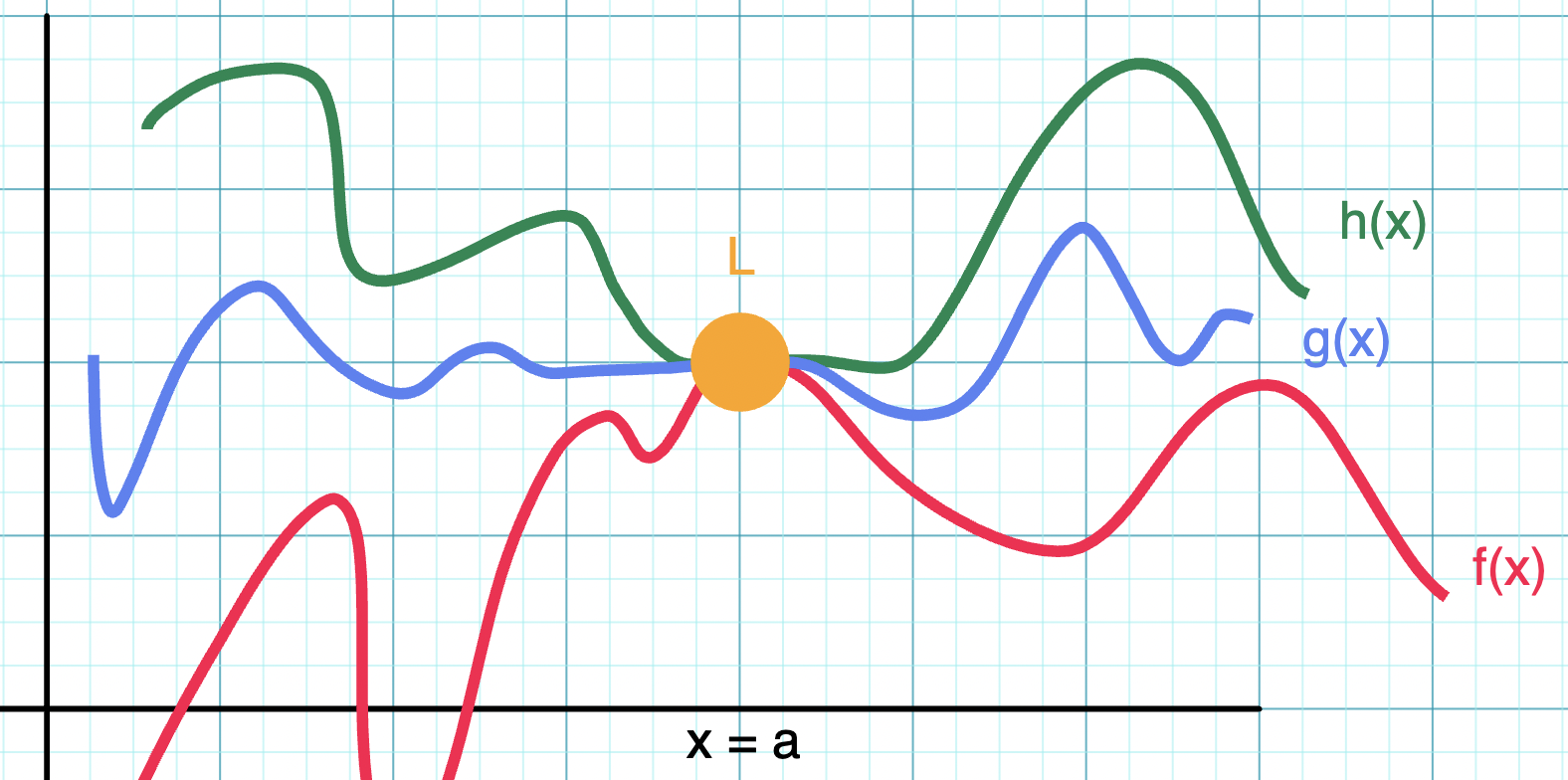
Graph representing squeeze theorem

Graph drawn using Virtual Graph Paper

We can see that the function $\textcolor {blue}{g(x)}$ is sandwiched between $\textcolor {red}{f(x)}$ and $\textcolor {green}{h(x)}$, so it must follow the same rule in the shown interval. $\lim_{{x \to a}} g(x) = \textcolor{orange}{L}$

---

🧮 Squeeze Theorem Practice Problems

Let’s work on a few questions and make sure we have the concept down!

1) Squeeze Theorem Logic

Functions $g$ and $h$ are twice-differentiable functions with $g(2) = h(2) = 4.$ It is known that $g(x) < h(x)$ for $1 < x < 3$. Let k be a function satisfying $g(x) \leq k(x) \leq h(x)$ for
$1 < x < 3$. Is $k$ continuous at $x = 2$? Justify your answer.

Once you’re ready, keep on reading to see how to approach this question. ⬇️

If functions $g$ and $h$ are twice-differentiable, they must be continuous. Therefore, $\lim_{{x \to 2}} g(x) = 4$ and $\lim_{{x \to 2}} h(x) = 4$. Since $g(x) \leq k(x) \leq h(x)$ and the conditions for continuity are met, the squeeze theorem for $k(x)$ applies at $x = 2$. So, $\lim_{{x \to 2}} k(x) = 4$ .

Since $4 = g(2) < k(2) < h(2) = 4$, $k(2)$ must equal $4$.

We can then conclude that $k(x)$ is continuous at $x = 4$ because $\lim_{{x \to 2}} k(x) = k(2) = 4$ . Brush up on continuity rules with this guide here: Confirming Continuity Over an Interval.

This question is from the 2019 AP Calculus AB examination administered by College Board. All credit to College Board. Way to go! 👏

2) Computing a Limit Using Squeeze Theorem

Find the limit of the function $\textcolor{blue}{g(x) = x\cos\left(\frac{1}{x}\right)}$ as $x$ approaches 0, using the Squeeze Theorem.

In this case, we can use the fact that $-1 < \cos\left(\frac{1}{x}\right) < 1$ for all $x$ to create a bounding function.

Multiply the inequality by $x$, and then consider the bounding functions $\textcolor{red}{f(x) = -x}$ and $\textcolor{green}{h(x) = x}$ so that $-x < x\cos\left(\frac{1}{x}\right) < x$.

Since $f(x) \leq g(x) \leq h(x)$ , and the functions are known to be continuous, the Squeeze Theorem can be applied. Let’s check the limits of the bounding functions as they approach 0 to see if they squeeze $g(x)$ at $x = 0$.

$\lim_{{x \to 0}} f(x) = \lim_{{x \to a}} -x = 0$

$\lim_{{x \to 0}} h(x) = \lim_{{x \to a}} x = 0$

Because $\lim_{{x \to 0}} f(x) = \lim_{{x \to 0}} h(x) = 0$, the Squeeze Theorem holds true, and…

$$\lim_{{x \to 0}} g(x) = \lim_{{x \to 0}} x\cos\left(\frac{1}{x}\right) = 0$$

Check out the graph below to confirm our answer visually!

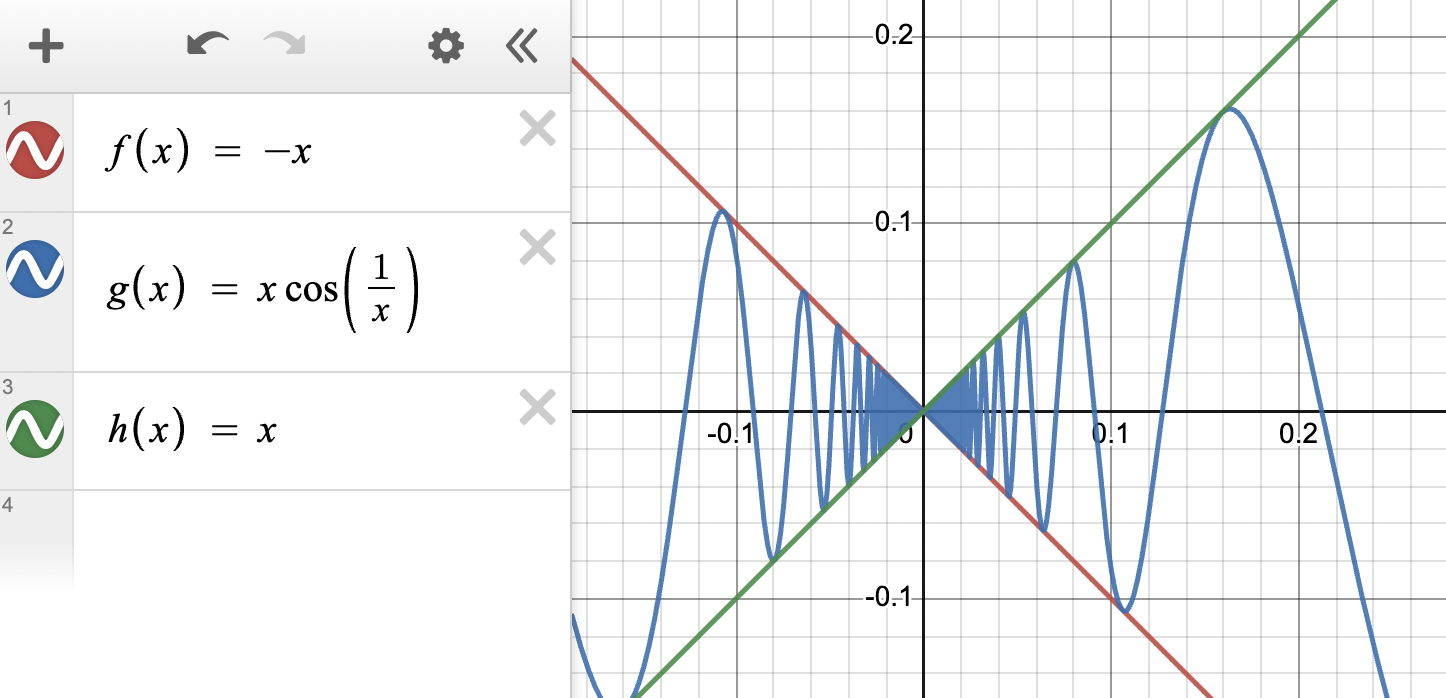
Graph proving $\lim_{{x \to 0}}x\cos\left(\frac{1}{x}\right) = 0$ by the Squeeze Theorem

Graph created with Desmos

You nailed it! This was a tough one. 💪

---

🌟 Closing

Great work! 🙌 The squeeze theorem is a key foundational idea for AP Calculus. You can anticipate encountering questions involving limits and the squeeze theorem on the exam, both in multiple-choice and as part of a free response.

Encouraging GIF with animated ice cream

Image Courtesy of Giphy

If you’d like some steps to follow, here they are:

1. 🤔 Identifying the Function: Recognize the function for which you need to determine the limit.
2. 👀 Finding the 'Squeeze' Functions: Locate two functions that 'squeeze' the given function between them.
3. 🏁 Ensuring Known Limits: Confirm that the limits of the 'squeezing' functions are known as x approaches the same value.

You got this! 🤩