In this section of the AP Calculus BC course, we will learn how to find the length of a smooth, planar curve, also known as the arc length. Then, we will look at how we can find the distance an object has traveled using the arc length of a curve. Finally, we’ll provide some practice problems so you can master this topic. Let’s get started!

🎢 What is Arc Length?

Before we dive into the process of computing arc length, let's clarify the fundamental concept behind it. In calculus, the arc length of a curve is the measure of the distance along the curve. You can think of it as tracing the curve with a string and then straightening the string—the length of that string is the arc length. For example, consider a roller coaster at an amusement park. The total length of the track of the roller coaster—including all the crazy twists, turns, and loop-the-loops—is the arc length of that track. Each segment of the track contributes to the overall arc length, offering a precise way to quantify the distance covered during the exhilarating ride.

Visualization of arc length.

GIF courtesy of Wikipedia.

---

〰️ How To Find the Arc Length of a Curve

Now, let's equip ourselves with the mathematical tools to calculate the arc length of a function. The arc length $S$ of a smooth, planar curve given by $y=f(x)$ from $x=a$ to $x=b$ is determined by the formula:

$$S=\int_a^b \sqrt{1+[f'(x)]^2} dx$$

This formula may look complex at first, but it breaks down into manageable steps that any great calculus student, such as yourself, can accomplish! Let’s work our way through this formula from the innermost expression outwards:

• $f'(x)$: The derivative of the function you are given with respect to $x$.
• $[f'(x)]^2$: The square of the derivative you just found.
• $1+[f'(x)]^2$: The sum of one and the square of the derivative.
• $\sqrt{1+[f'(x)]^2}$: The square root of the sum.
• $\int_a^b \sqrt{1+[f'(x)]^2} dx$: The sum of all the little line segments along a curve between two endpoints. Now that you understand the components of the formula, let’s understand why it works. The term inside the square root stems from the Pythagorean Theorem. The form of the Pythagorean theorem being referred to here is $c=\sqrt{a^2+b^2}$, used to find the hypotenuse of a right triangle.

In the arc length formula, 1 represents the square of the length along the x-axis, and $[f'(x)]^2$ represents the square of the length along the y-axis. Then, the hypotenuse of this triangle becomes a small segment on the curve. This way, the integrand (term inside the integral) calculates the length of an infinitesimally small section of the curve, and integrating this expression adds up all the small lengths to give us the entire arc length for that segment of the curve. Pretty smart, right? 🧠

---

🚗 Using Arc Length to Calculate Distance Traveled

Now that we know how to calculate the arc length of a function, let's explore how it ties into real-world scenarios, particularly in determining the distance traveled by an object.

Distance traveled is a quantity that represents the total length of the path covered by an object in motion. It is a measure of the actual ground covered, irrespective of the direction in which the object moves. Even if the object moves backwards, the distance it has traveled will still increase. Below is an image showing how the distance traveled differs from the displacement of an object. The distance traveled is always a non-negative value.

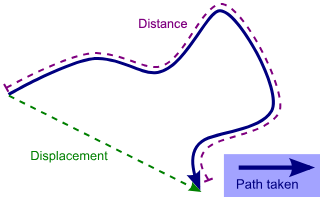
The displacement vs. the distance traveled.

Image courtesy of Khan Academy.

Arc length is crucial in calculus because it provides a way to calculate the distance traveled along a curve, even when the curve is complex and continuously changing. Traditional measures, such as the straight-line distance between two points, fall short when dealing with curves. Arc length, on the other hand, embraces the curve's complexity, making it an indispensable tool for understanding and analyzing various phenomena in mathematics and physics.

To set the stage, imagine an object moving along a curve described by $y=f(x)$. The arc length $S$, calculated using our formula, represents the total distance traveled by the object along the curve. For example, consider a car moving along a winding road given by the function $y=x^2$ from $x=0$ to $x=3$. By calculating the arc length, we can precisely determine the total distance covered by the car on this segment of the road.

🪜Steps Using Arc Length to Calculate Distance Traveled

Here is a step-by-step calculation:

1. 💫 Define the Function: $f(x)=x^2$
2. 🎯 Find $f'(x)$: $f'(x)=2x$
3. ✍️ Apply the Arc Length Formula: $S=\int_0^3 \sqrt{1+(2x)^2} dx$
4. ⛳ Evaluate the Integral: Use your calculus skills to compute the arc length. Using u-substitution with $u=1+4x^2$ and $du=8xdx$, You should get $S=\frac{1}{12}(13\sqrt{13} - 1)$ or approximately 3.823 units.

Let’s do two more problems for additional practice!

---

🖊 Arc Length Practice

Try to tackle the questions before proceeding to see the answers.

❓ Arc Length Question 1

Consider the curve represented by the equation $y=x^3$, where x is between 0 and 2.

To find the arc length of this curve, we need to first find the derivative of the curve, which is $y'=3x^2$. Next, we use the formula for arc length, $S=\int_a^b \sqrt{1+[f'(x)]^2} dx$ from x = 0 to x = 2. After evaluating the integral, we find that the arc length of the curve is approximately 3.72 units.

❓ Arc Length Question 2

A particle moves along the curve represented by the equation $f(x)=x^2+1$, where x is between 0 and 2.

To find the distance traveled by the particle, we use the formula for arc length, $S=\int_a^b \sqrt{1+[f'(x)]^2} dx$ from x = 0 to x = 2. After evaluating the integral, we find that the distance traveled by the particle is approximately 5.83 units.

---

➿ Conclusion

The Arc Length of a Smooth, Planar Curve and Distance Traveled is a crucial topic in AP Calculus BC that involves finding the length of a curve or the distance traveled by a particle along a curve. To find the arc length of a curve, we need to find the derivative of the curve and use the formula for arc length, $S=\int_a^b \sqrt{1+[f'(x)]^2} dx$. To find the distance traveled by a particle, we can use the same formula in the context of the problem. Evaluating these integrals requires a good understanding of derivatives, integrals, and the formula for arc length. With proper practice and application, you will become proficient in this topic and excel on the AP Calculus BC exam! 🍀